Home › Archief › Nationale en Regionale Olympiades › België › JWO › 2007 › vierkantjes

vierkantjes

Tags:

Opgave - JWO 2007 dag 1 vraag 4

Beschouw de vierkanten $ABCD, CEDF$ en $BGHE$ waarbij $F$ in $ABCD$ ligt en $C$ in $BGHE.$
Bewijs dat $|AC| = |CH|$ bij die constructie.

Oplossing

Ingediend door Rebhood

Als het vierkant $ABCD$ met zijde $2x$ beschouwen dan is de verschuiving van $A$ naar $C$ gelijk aan: $2x\downarrow , 2x\rightarrow$
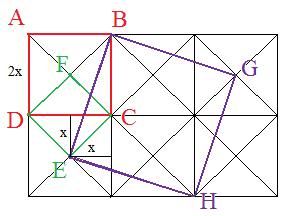
De verschuiving van $C$ naar $H$ is gelijk aan de verschuiving van $C$ naar $B$ naar $E$ naar $H$
De verschuiving van $C$ naar $H$ $=$ $2x\uparrow, (3x\downarrow , 1x \leftarrow) ,(1x \downarrow, 3x\rightarrow)=2x\downarrow, 2x\rightarrow$
$\Rightarrow \overrightarrow{AC}=\overrightarrow{CH}$
$\Rightarrow |AC|=|CH|$
Ter verduidelijking volgende tekening:

Ingediend door Toon

$I$ is het midden van $[AB]$.
$J$ is het midden van $[CD]$
$K (\neq I)$ ligt op $IJ$ op de afstand $|IJ|$ van $J$.

$|IF|=|FJ|=|JE|=|EK|$

$\angle EIB=90^o$
$\angle IEB=90^o-\angle EBI$

$\angle KEH=90^o-\angle IEB=\angle EBI$

$\triangle BIE \cong \triangle EKH \left\{
\begin{array}{l l}
Z \quad |EH|=|BE|\\
H \quad \angle KEH=\angle IBE\\
Z \quad |EK|=|BI|\\
\end{array} \right.
$

$|IE|=3|IB| \Rightarrow |KH|=3|KE|=3|IB|$

$L$ is het snijpunt van $BC$ en $KH$

$|HL|=|KH|-|KL|=|KH|-|IB|=2|IB|=|AB|$ (1)

$|CL|=|KJ|=|IJ|=|BC|$ (2)

$\triangle ABC \cong \triangle HLC \left\{
\begin{array}{l l}
Z \quad (1)\\
H \quad B=L\\
Z \quad (2)\\
\end{array} \right.
$
Dus:
$|AC|=|HC|$

Ingediend door Jeroen

Gemaakt met afb. van Rebhood:

In $\bigtriangleup ACE$ en $\bigtriangleup HCE$:
$|AC|$²$ = (2x)$²$ + (2x)$²
$|AC| = 2\sqrt{2}x$
(volgens pythagoras)
$|CE| = |FC| = 0,5(2\sqrt{2})x = \sqrt{2}x$ (Diagonalen in vierkanten snijden mekaar middendoor)
$|AE|$² $= |CE|$²$ + |AC|$² = $2x$²$ + 8x$²$ = 10x$²
$|AE| =\sqrt{10}x$

$|BE| = |AE| = $wortel$(10)x$ (gelijke zijden gelijkbenige driehoek, want diagonalen vierkant snijden mekaar middendoor)
$|HE|=|BE| = |AE|$ (zijden vierkant zijn even lang)
$\angle{ ACE} = \angle{HCE}$ ($C$ van $\bigtriangleup ACE = 90^{\circ}$, van $\bigtriangleup HCE =$ supplementaire hoek van een rechte hoek -> $90$°)
$|CE| = |CE$| (gemeenschappelijke zijde)
=> $\bigtriangleup ACE \cong \bigtriangleup HCE$ (volgens kenmerk Schuine zijde – rechte zijde in een rechthoekige driehoek)
=> $|CH| = |AC|$ (overeenkomstige zijden in congruente driehoeken)
****
opm.: deze opl. gaat er al van uit dat $A,C,H$ collineair zijn wat beter wordt bewezen met bvb. gelijkvormigheid tussen $\triangle{ACE},\triangle{HCE}$ met $HHZ$ om alle punten te krijgen.
...