Home › Archief › Nationale en Regionale Olympiades › België › JWO › 2004 › som van stambreuken

som van stambreuken

Tags:

Opgave - JWO 2004 dag 1 vraag 4

Vind alle koppels natuurlijke getallen $(a,b)$ zodat $\frac{1}{a}+\frac{1}{b}=\frac{1}{2004}$

Oplossing

Ingediend door Rebhood

$\frac{1}{2004} = \frac{y+z}{2004*(y+z)}$

$\frac{1}{2004} = \frac{y}{2004*(y+z)} + \frac{z}{2004*(y+z)}$

$\frac{1}{2004} = \frac{1}{\frac{2004}{y}*(y+z)} + \frac{1}{\frac{2004}{z}*(y+z)}$

omdat deze noemers natuurlijke getallen moeten zijn zijn $z,y$ delers van $2004$

zij $X1$ en $X2$ delers van 2004
dan geldt:
$a=\frac{2004}{X1} * (X1+X2)$

$b= \frac{2004}{X2} * (X1+X2)$

dus dan zoeken we alle mogelijke $a$'s en $b$'s

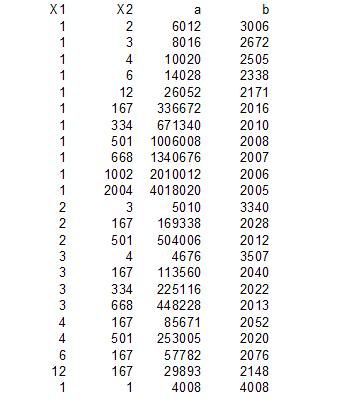
Uiteraard is het wisselen van $a$ en $b$ ook een oplossing

Ingediend door barto

De klassieke methode gaat als volgt:
We kunnen $\frac1{2004}=\frac1a+\frac1b$ herschrijven als $ab=2004a+2004b$, of nog, $ab-2004a-2004b+2004^2=2004^2$ wat we kunnen ontbinden als $(a-2004)(b-2004)=2004^2$. De vraag is nu gewoon wanneer het product van twee gehele getallen $2004^2$ is. Merk op dat de factoren $a-2004$ en $b-2004$ niet beide negatief kunnen zijn: het gegeven dat $a,b>0$ betekent dat de absolute waarde van die factoren dan hoogstens $2003$ zou kunnen zijn, en het product dus kleiner dan $2004^2$.
$a$ en $b$ zijn dus van de vorm $a=c+2004$ en $b=d+2004$, met $cd=2004^2$ en $c,d>0$. (Bijvoorbeeld $a=2005$ en $b=2004^2+2004$, een oplossing die niet uit de methode van rebhood volgt.)
We kunnen $2004$ ontbinden als $2^2\cdot3\cdot167$, zodat $2004^2=2^4\cdot3^2\cdot167^2$. De delers van $2004^2$ zijn dus $1,2,2^2,2^3,2^4,3,3^2,2\cdot3,2\cdot3^2,2^2\cdot3$ enzovoort. Er zijn er $45$ in totaal dus die ga ik niet allemaal opschrijven, ik geloof trouwens niet dat op die JWO echt werd gevraagd om alle oplossingen uit te schrijven. Het antwoord is gewoon $a=2004+c$ en $b=2004+d$, met $cd=2004^2$ en $c,d>0$. Alle mogelijkheden haal je uit de priemontbinding van $2004^2$, het aantal oplossingen $(a,b)$ is $45$.