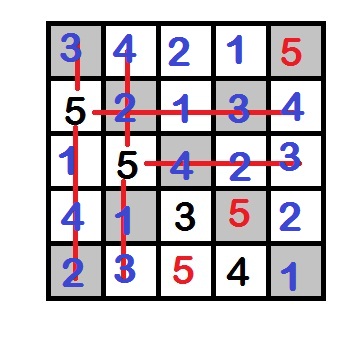
5x5 vierkant

Als de score van de vier vierkantjes onder de linksboven-rechtsonder diagonaal 20 is, dan moeten ze allevier 5 zijn. Maar, als ze 5 zijn, kan er geen enkel vierkantje op de linksboven-rechtsonder diagonaal 5 zijn, en dat is strijdig met het gegeven (beide diagonalen bevatten alle vijf de cijfers exact een keer).
We proberen of als maximale score 19 mogelijk is:
3 vakjes net onder de linksboven-rechtsonder diagonaal zijn $5$ en de andere een $4$,
dit betekent dat op de diagonaal zelf er 3 vakjes zijn die op een rij met een 5 liggen en omdat de 3 kolommen die een 5 bevatten niet de 3 zelfde hokjes kunnen bevatten ( neem de meest linkse kolom met een 5, en bekijk het vakje erboven, dat zat niet in een zelfde rij, maar mag ook geen 5 bevatten), de plaats van de 5 op die diagonaal is dan éénduidig bepaald.
Bekijk nu de andere diagonaal, 3 vakjes liggen op een 5-rij van de score en mogen geen 5 zijn en terug is er 1 vakje die op eenzelfde kolom ligt extra.
De $4^e$ 5 die we plaatsten, mag echter in geen zelfde kolom of rij van een vorig vakje liggen en zorgt dus dat het laatste vakje op de rechtsboven-linksonder diagonaal ook geen 5 mag zijn, zodat het onmogelijk is hier een 5 te plaatsen zoals gevraagd houdend aan de overige voorwaarden.
18 voldoet niet, er zouden dan 2 4'en en 2 5'en in de score moeten liggen, maar bekijk hiervoor de $3$ mogelijke configuraties;

In tekening 1 en 2 zijn de enige mogelijke 5 en 4 op de rechtsboven-linksonder diagonaal op dezelfde plaats. En in tekening 3 zien we dat de enige plaatsen op de linksboven-rechtsonder voor een 4 linksboven en rechtsonder zijn. We weten dus dat de enige mogelijke 4 op de rechtsboven-linksonder diagonaal in het 4de hokje op de 2de rij ligt. Daaruit volgt dat de 2 resterende 4en in het hokje linksboven en rechtsonder liggen, wat niet kan omdat ze op dezelfde diagonaal zijn.

Tot slot tonen we dat het met $17$ gaat, waardoor dit het maximum is